To apply your skills in algorithmic optimization through the implementation of improved prime number calculating programs.

A concept in Computer Science curriculum is the notion of computational/algorithmic complexity.

Basically, a solution to a problem exists on a spectrum of efficiency (typically constrained by time vs. space). Once you've hashed out an implementation:

• if optimizing for (or trying to take up less) time, the code size tends to grow or become more complex.
• if optimizing for (or trying to take up less) space, the program runtime can grow.

Let it be clear: using modern computers bound by fourth dimensional constraints, we cannot write solutions without some foothold in both space and time (any program has statements in it that accomplish the task at hand (space occupied), and that same program takes time to run (even if it happens rather quickly)). What we can do is influence where on the space-time spectrum our implementation falls, and if done strategically for the particular constraint at hand, can aid us in achieving desired improvements in program efficiency.

In the previous projects, we focused on algorithms that were more constrained by time- taking progressively more time the larger the data set to be processed. These time-constrained algorithms also happen to be the type of algorithm you're most familiar with (or at least, were indoctrinated into thinking with…) your third grade self, on the other hand, potentially would have found more familiarity with the space-constrained methods this project will explore.

So in contrast to time-constrained approaches we have space-constrained approaches, which will utilize more space (ie allocating memory) in the solving of the program to the benefit of requiring less time.

We can never be entirely time- or space-free… some element of the other will always be present. But by embracing the advantages of an approach, we can really make an impact in the desired area.

What we will be looking at in this project is a type of prime number calculating algorithm known as a sieve. It will make strategic use of space to aid us in the solving of the problem instead of exclusively relying on time.

Of note, the “mainstream” prime number computing efforts typically make use of sieves.

Following will be the optimized algorithms I'd like you to implement for comparison with all the others.

For this project, please assume the following:

• unless otherwise specified, you are doing all values (odds AND evens).
• if you exceed 64 million and get “–error!—” from primerun that's okay. I have memory limits in place (just like I have time limits in place).
• as the space-based approach to solving our prime number computation problem is fundamentally different from those we took in previous projects, you will want to look to start from scratch. Trying to reuse old code and shoehorn it into what effectively amounts to an entirely different paradigm will create a lot of problems.

But, the conceptual level we'll be pursuing will be the space-based equivalent of primebrute/primebrk, that is, no fancy optimizations for odd numbers, nor the sqrt() trick, just straight up processing of the values that need to be processed.

Your next program, and first sieve, will be the Sieve of Eratosthenes. Perhaps among the best and likely longest-known sieves, its origins date from antiquity.

This sieve, instead of calculating to determine the eligibility of a prime, works in a manner of marking off patterns of values that cannot be prime (so, it is composite-focused in approach vs. prime-focused).

In order for it to work, we must store all the values we're processing so we can obtain what is left when done– what remains are the prime values.

Here is the wikipedia page: https://en.wikipedia.org/wiki/Sieve_of_Eratosthenes

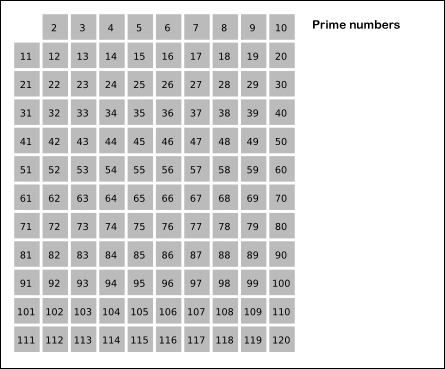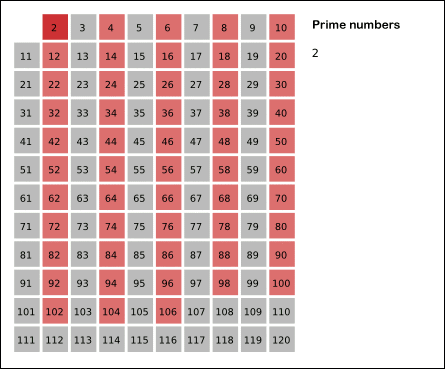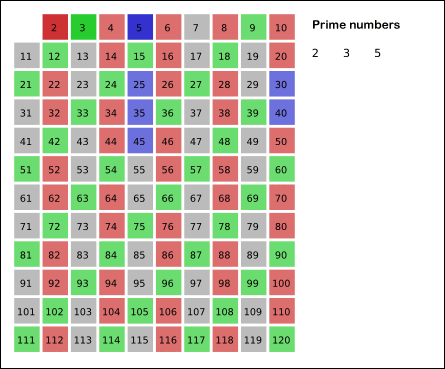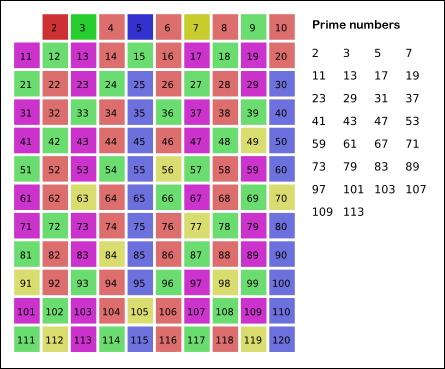
Here is an animated image of this sieve in action (from wikipedia):

This YouTube video may also be helpful:

Sieve of Eratosthenes

A basic outline of the algorithm (again, from the wikipedia page):

To find all the prime numbers less than or equal to a given integer n by Eratosthenes' method:

1. Create a list of consecutive integers from 2 through n: (2, 3, 4, …, n).
2. Initially, let p equal 2, the smallest prime number.
3. Enumerate the multiples of p by counting to n from 2p in increments of p, and mark them in the list (these will be 2p, 3p, 4p, … ; the p itself should not be marked).
4. Find the first number greater than p in the list that is not marked. If there was no such number, stop. Otherwise, let p now equal this new number (which is the next prime), and repeat from step 3.

When the algorithm terminates, the numbers remaining in the list that are not marked are the primes below n.

This is a space-constrained algorithm, therefore we will need a chunk of space to store these values. Think about what a lot of this looks like with respect to how you know how to organize data.

Taking the primesoe codebase, enhance it to do odds-only processing, ideally considering overall storage used.

Taking the primesoe codebase, enhance it to utilize the sqrt() (or sqrt()-less square root) trick.

Compared to the brute/brk algorithms from the previous projects, the performance differences between using sqrt() and approximating the square root should be minimal. You are free to utilize either approach in your implementation for this project.

NOTE: this variant is still to process all values (odd and even).

NOTE: if you are curious in comparing actual performance between sqrt() and approximated square root, primerun will recognize the following program names:

• primesoesrt
• primesoesrtopt

Taking the primesoe codebase, enhance it to do odds-only processing AND utilize the sqrt() (or sqrt()-less square root) trick.

Compared to the brute/brk algorithms from the previous projects, the performance differences between using sqrt() and approximating the square root should be minimal. You are free to utilize either approach in your implementation for this project.

NOTE: if you are curious in comparing actual performance between sqrt() and approximated square root for this odds-processing variant, primerun will recognize the following program names:

• primesoesrtodd
• primesoesrtoptodd

It is your task to write four Sieve of Eratosthenes-oriented prime number calculating programs:

1. primesoe.c: using the space-oriented sieve algorithm (baseline sieve)
2. primesoeodd.c: applying the odds-only processing to the sieve of Eratosthenes
3. primesoesrt.c: applying the sqrt() trick to sieve of Eratosthenes
4. primesoesrtodd.c: applying BOTH odds-only processing and sqrt() trick to sieve of Eratosthenes

Your programs should:

• obtain 2-4 parameters from the command-line (see command-line arguments section below).
  • check to make sure the user indeed supplied enough parameters, and exit with an error message if not.
  • argv[1]: maximum quantity of primes to calculate (your program should run until it discovers that many primes).
    • this value should be an integer value, greater than or equal to 0.
      • if argv[1] is 0, disable the quantity check, and rely on provided lower and upper bounds (argv[4] would be required in this case).
  • argv[2]: reserved for future compatibility; for now, assume it is 1.
  • argv[3]: conditionally optional lower bound (starting value). Most of the time, this will probably be 2, but should be a positive integer greater than or equal to 2. This defines where you program will start its prime quantity check from.
    • if omitted, assume a lower bound of 2.
    • if you desired to specify an upper bound (argv[4]), you obviously MUST provide the lower bound argument under this scheme.
  • argv[4]: conditionally optional upper bound (ending value). If provided, this is the ending value you'd like to check to.
    • If doing a quantity run (argv[1] NOT 0), this value isn't necessary.
    • If doing a quantity run AND you specify an upper bound, whichever condition is achieved first dictates program termination. That is, upper bound could override quantity (if it is achieved before quantity), and quantity can override the upper bound (if it is achieved before reaching the specified upper bound).
  • for each argument: you should do a basic check to ensure the user complied with this specification, and exit with a unique error message (displayed to STDERR) otherwise:
    • for insufficient quantity of arguments, display: PROGRAM_NAME: insufficient number of arguments!
    • for invalid argv[1], display: PROGRAM_NAME: invalid quantity!
    • for invalid argv[2], display: PROGRAM_NAME: invalid value!
    • for invalid argv[3], display: PROGRAM_NAME: invalid lower bound!
      • if argv[3] is not needed, ignore (no error displayed not forced exit, as it is acceptable defined behavior).
    • for invalid argv[4], display: PROGRAM_NAME: invalid upper bound!
      • if argv[4] is not needed, ignore (no error displayed nor forced exit, as it is acceptable defined behavior).
    • In these error messages, PROGRAM_NAME is the name of the program being run; this can be accessed as a string stored in argv[0].
  • please take note in differences in run-time, contemplating the impact the various algorithms/optimizations have on performance.
• start your stopwatch (see timing section below).
• perform the correct algorithm against the input(s) given.
• display to STDOUT (file pointer stdout) the prime numbers calculated.
• stop your stopwatch. Calculate the time that has transpired (ending time minus starting time).
• output the processing run-time to STDERR (file pointer stderr).
• your output MUST conform to the example output in the execution section below. This is also a test to see how well you can implement to specifications. Basically:
  • as primes are being displayed, they are space-separated (first prime hugs the left margin), and when all said and done, a newline is issued.
  • the timing information will be displayed in accordance to code I will provide below (see the timing section).

For those familiar with the grabit tool on lab46, I have made some skeleton files and a custom Makefile available for this project.

To “grab” it:

lab46:~/src/cprog$ grabit cprog pnc2
make: Entering directory '/var/public/SEMESTER/cprog/pnc2'
‘/var/public/SEMESTER/cprog/pnc2/Makefile’ -> ‘/home/USERNAME/src/cprog/pnc2/Makefile’
‘/var/public/SEMESTER/cprog/pnc2/primesoe.c’ -> ‘/home/USERNAME/src/cprog/pnc2/primesoe.c’
‘/var/public/SEMESTER/cprog/pnc2/primesoeodd.c’ -> ‘/home/USERNAME/src/cprog/pnc2/primesoeodd.c’
‘/var/public/SEMESTER/cprog/pnc2/primesoesrt.c’ -> ‘/home/USERNAME/src/cprog/pnc2/primesoesrt.c’
‘/var/public/SEMESTER/cprog/pnc2/primesoesrtodd.c’ -> ‘/home/USERNAME/src/cprog/pnc2/primesoesrtodd.c’
make: Leaving directory '/var/public/SEMESTER/cprog/pnc2'
lab46:~/src/cprog$ cd pnc2
lab46:~/src/cprog/pnc2$ ls
Makefile  primesoe.c  primesoeodd.c  primesoesrt.c  primesoesrtodd.c
lab46:~/src/cprog/pnc2$ 

Furthermore, if your pnc2/ project directory is next to a pnc1/ and pnc0/ directory, each containing those project's specific prime variants, you can symlink them into the current project directory with a make link:

lab46:~/src/cprog/pnc2$ make link
‘./primebrute.c’ -> ‘../pnc0/primebrute.c’
‘./primebrk.c’ -> ‘../pnc0/primebrk.c’
‘./primebrkodd.c’ -> ‘../pnc1/primebrkodd.c’
‘./primebrksrt.c’ -> ‘../pnc1/primebrksrt.c’
‘./primebrkoddsrt.c’ -> ‘../pnc1/primebrkoddsrt.c’
‘./primebrksrtopt.c’ -> ‘../pnc1/primebrksrtopt.c’
‘./primebrkoddsrtopt.c’ -> ‘../pnc1/primebrkoddsrtopt.c’
lab46:~/src/cprog/pnc2$ 

And, of course, your basic compile and clean-up operations:

• make: compile everything
• make debug: compile everything with debug support
• make clean: remove all binaries

Just another “nice thing” we deserve.

NOTE: You do NOT want to do this on a populated pnc2/ project directory– it will overwrite files. Only do this on an empty directory.

To automate our comparisons, we will be making use of command-line arguments in our programs. As we have yet to really get into arrays, I will provide you same code that you can use that will allow you to utilize them for the purposes of this project.

We don't need any extra header files to use command-line arguments, but we will need an additional header file to use the atoi(3) function, which we'll use to quickly turn the command-line parameter into an integer, and that header file is stdlib.h, so be sure to include it with the others:

#include <stdio.h>
#include <stdlib.h>

To accept (or rather, to gain access) to arguments given to your program at runtime, we need to specify two parameters to the main() function. While the names don't matter, the types do.. I like the traditional argc and argv names, although it is also common to see them abbreviated as ac and av.

Please declare your main() function as follows:

int main(int argc, char **argv)

The arguments are accessible via the argv array, in the order they were specified:

• argv[0]: program invocation (path + program name)
• argv[1]: our maximum / upper bound

Although I'm not going to require extensive argument parsing or checking for this project, we should check to see if the minimal number of arguments has been provided:

    if (argc < 2)  // if less than 2 arguments have been provided
    {
        fprintf(stderr, "Not enough arguments!\n");
        exit(1);
    }

Finally, we need to put the argument representing the maximum value into a variable.

I'd recommend declaring a variable of type int.

We will use the atoi(3) function to quickly convert the command-line arguments into int values:

    max  = atoi(argv[1]);

And now we can proceed with the rest of our prime implementation.

Often times, when checking the efficiency of a solution, a good measurement (especially for comparison), is to time how long the processing takes.

In order to do that in our prime number programs, we are going to use C library functions that obtain the current time, and use it as a stopwatch: we'll grab the time just before starting processing, and then once more when done. The total time will then be the difference between the two (end_time - start_time).

We are going to use the gettimeofday(2) function to aid us in this, and to use it, we'll need to do the following:

In order to use the gettimeofday(2) function in our program, we'll need to include the sys/time.h header file, so be sure to add it in with the existing ones:

#include <stdio.h>
#include <stdlib.h>
#include <sys/time.h>

gettimeofday(2) uses a struct timeval data type, of which we'll need to declare two variables in our programs (one for storing the starting time, and the other for the ending time).

Please declare these with your other variables, up at the top of main() (but still WITHIN main()– you do not need to declare global variables).

    struct timeval time_start; // starting time
    struct timeval time_end;   // ending time

To use gettimeofday(2), we merely place it at the point in our code we wish to take the time.

For our prime number programs, you'll want to grab the start time AFTER you've declared variables and processed arguments, but JUST BEFORE starting the driving loop doing the processing.

That call will look something like this:

    gettimeofday(&time_start, 0);

The ending time should be taken immediately after all processing (and prime number output) is completed, and right before we display the timing information to STDERR:

    gettimeofday(&time_end, 0);

Once we having the starting and ending times, we can display this to STDERR. You'll want this line:

    fprintf(stderr, "%10.6lf\n", time_end.tv_sec - time_start.tv_sec + ((time_end.tv_usec - time_start.tv_usec) / 1000000.0));

For clarity sake, that format specifier is “%10.6lf”, where the “lf” is “long float”, that is NOT a number one but a lowercase letter 'ell'.

And with that, we can compute an approximate run-time of our programs. The timing won't necessarily be accurate down to that level of precision, but it will be informative enough for our purposes.

Your program output should be as follows (given the specified range):

lab46:~/src/cprog/pnc2$ ./primesoe 32 1
2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 83 89 97 101 103 107 109 113 127 131
  0.000088
lab46:~/src/cprog/pnc2$ 

The execution of the programs is short and simple- grab the parameters, do the processing, produce the output, and then terminate.

You may notice a change with the sieves as compared to the other algorithms you've implemented with respect to performance- there will likely be a lower bound of performance, ie you have to exceed a certain threshold before the algorithm truly enters its power band, and then it may truly be a step-up in terms of performance.

To verify your program's correctness and view your implementation's performance, primerun will recognize the indicated program names listed above.

I'll hold off from posting actual primerun output; I want you to see the results without any expectations. Do know that the arrangement of programs (from left to right) is in order of worst to best performance based on my implementations.

If/when the runtime of a particular prime variant exceeds an upper threshold (likely to be set at 2 seconds), it will be omitted from further tests, and a series of dashes will instead appear in the output.

If you don't feel like waiting, simply hit CTRL-c and the script will terminate.

If the check is successful, you will see “OK” displayed beneath in the appropriate column; if unsuccessful, you will see “MISMATCH”.

To successfully complete this project, the following criteria must be met:

• Code must compile cleanly (no warnings or errors)
• Output must be correct, and match the form given in the sample output above.
• Code must be nicely and consistently indented (you may use the indent tool)
• Code must utilize the algorithm(s) presented above.
  • primesoe.c
  • primesoeodd.c
  • primesoesrt.c
  • primesoesrtodd.c
• Code must be commented
  • have a properly filled-out comment banner at the top
    • be sure to include any compiling instructions
  • have at least 20% of your program consist of //-style descriptive comments
• Output Formatting (including spacing) of program must conform to the provided output (see above).
• Track/version the source code in a repository
• Submit a copy of your source code to me using the submit tool.

To submit this program to me using the submit tool, run the following command at your lab46 prompt:

$ submit cprog pnc2 primesoe.c primesoeodd.c primesoesrt.c primesoesrtodd.c
Submitting cprog project "pnc2":
    -> primesoe.c(OK)
    -> primesoeodd.c(OK)
    -> primesoesrt.c(OK)
    -> primesoesrtodd.c(OK)

SUCCESSFULLY SUBMITTED

You should get some sort of confirmation indicating successful submission if all went according to plan. If not, check for typos and or locational mismatches.

What I will be looking for:

78:pnc2:final tally of results (78/78)
*:pnc2:submit all programs correctly perform argument checking [2/2]
*:pnc2:primesoe.c no negative compiler messages [2/2]
*:pnc2:primesoe.c implements only specified algorithm [8/8]
*:pnc2:primesoe.c adequate indentation and comments [3/3]
*:pnc2:primesoe.c output conforms to specifications [3/3]
*:pnc2:primesoe.c primerun runtime tests succeed [3/3]
*:pnc2:primesoeodd.c no negative compiler messages [2/2]
*:pnc2:primesoeodd.c implements only specified algorithm [8/8]
*:pnc2:primesoeodd.c adequate indentation and comments [3/3]
*:pnc2:primesoeodd.c output conforms to specifications [3/3]
*:pnc2:primesoeodd.c primerun runtime tests succeed [3/3]
*:pnc2:primesoesrt.c no negative compiler messages [2/2]
*:pnc2:primesoesrt.c implements only specified algorithm [8/8]
*:pnc2:primesoesrt.c adequate indentation and comments [3/3]
*:pnc2:primesoesrt.c output conforms to specifications [3/3]
*:pnc2:primesoesrt.c primerun runtime tests succeed [3/3]
*:pnc2:primesoesrtodd.c no negative compiler messages [2/2]
*:pnc2:primesoesrtodd.c implements only specified algorithm [8/8]
*:pnc2:primesoesrtodd.c adequate indentation and comments [3/3]
*:pnc2:primesoesrtodd.c output conforms to specifications [3/3]
*:pnc2:primesoesrtodd.c primerun runtime tests succeed [3/3]