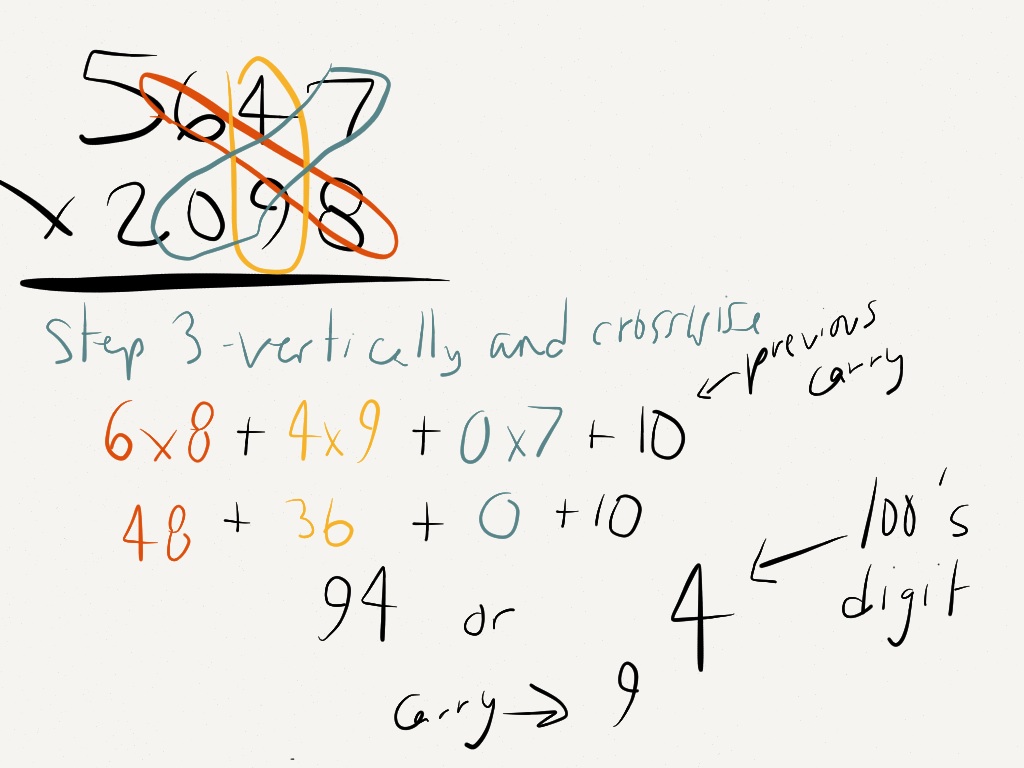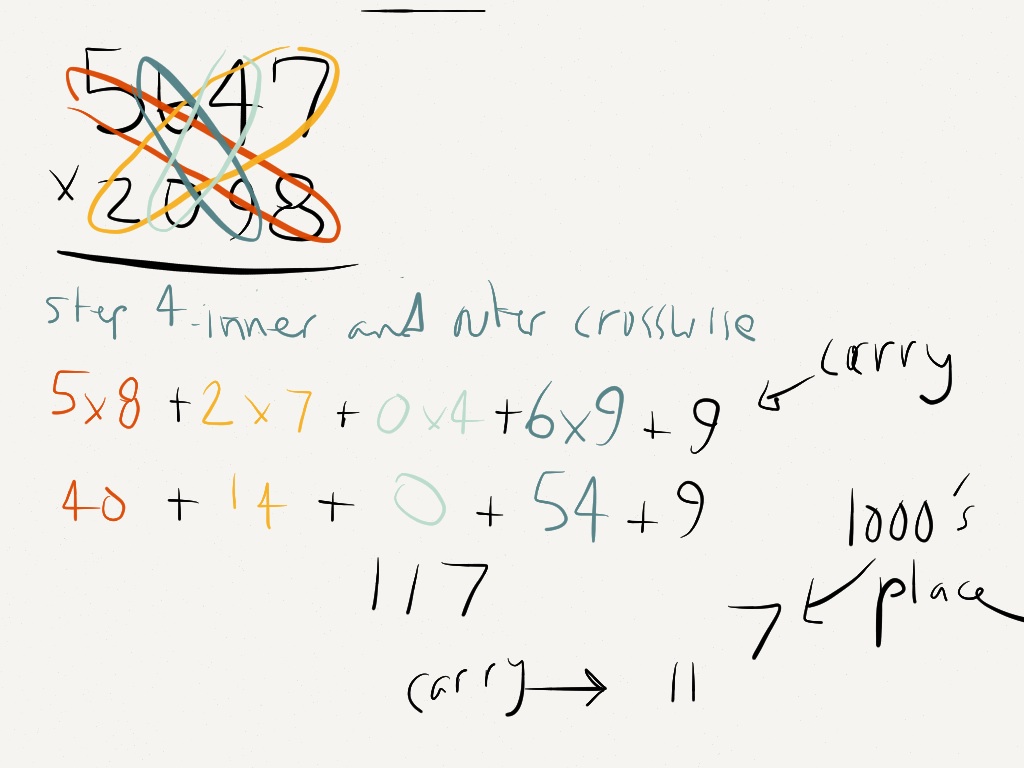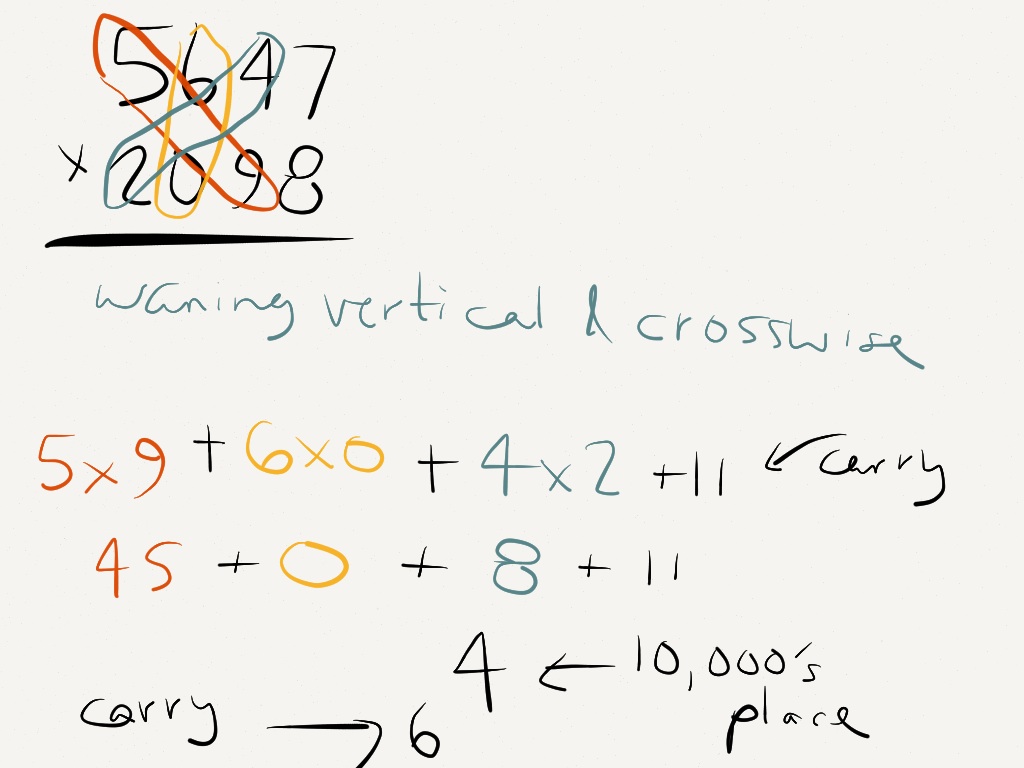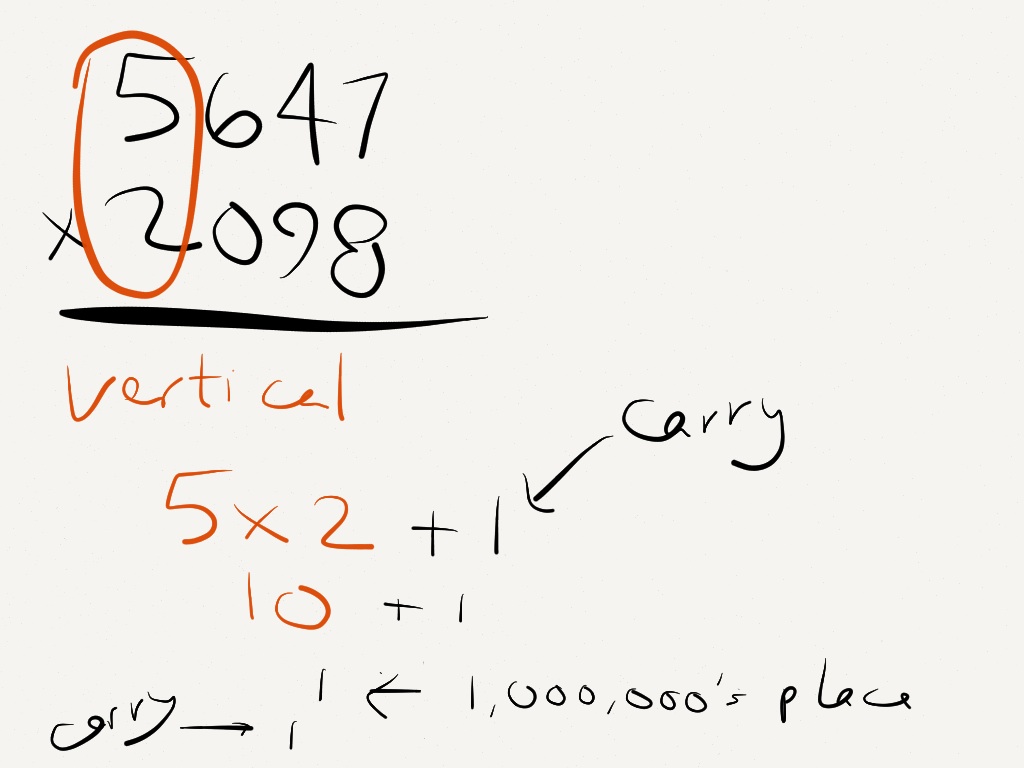projects
| cci0 (due 20170826) |
| wcp1 (due 20170826) |
| dtr0 (due 20170830) |
| wcp2 (due 20170902) |
| sof0 (due 20170906) |
| wcp3 (due 20170909) |
| dow0 (due 20170913) |
| wcp4 (due 20170916) |
| mbe0 (due 20170920) |
| wcp5 (due 20170923) |
| cbf0 (due 20170927) |
| wcp6 (due 20170930) |
| cos0 (due 20171004) |
| wcp7 (due 20171007) |
| pnc0 [metrics] (due 20171018) |
| mbe1 (BONUS – due 20171018) |
| wcp8 (due 20171021) |
| pnc1 [metrics] (due 20171025) |
| wcp9 (due 20171028) |
| gfo0 (due 20171101) |
| wcpA (due 20171104) |
| gfo1 (due 20171108) |
| wcpB (due 20171111) |
| gfo2 (due 20171115) |
| wcpC (due 20171118) |