As abstraction is a key focus of Computer Science and Data Structures, our first knowledge assessment, dska0, presented an activity befitting of such concepts.

Taking a page from our on-going linked list explorations, this activity presented a modified linked list, specifically of the form:

struct node {
    unsigned char data;
    struct node *prev;
};

That is, a singly-linked node that is intended to linked to its previous neighbor, vs. its next neighbor, as the bulk of our in-class examples and projects have focused on.

So from an implementation point-of-view, yeah, a bit different (inverted, even), but conceptually? No different at all.

To make sure we understand the scope of what was being asked, we were to implement (at a minimum) the append() operation for this previous-oriented singly-linked list.

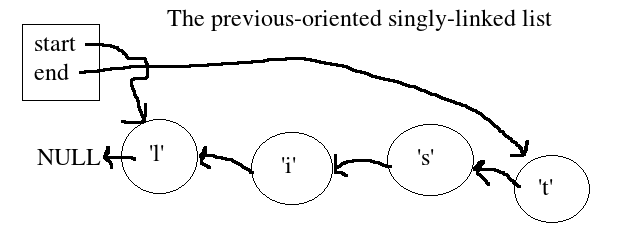
I drew a similar picture on the board of how the list is manifested:

Note that the NULL terminating the list is to the left of the list start… so again, an inversion or negation what we are used to seeing.

The trick here is that we still view this list from left to right– start is on the left (or beginning), and end is on the right (the contextual end). In this scenario, the connections work against the grain when using the list.

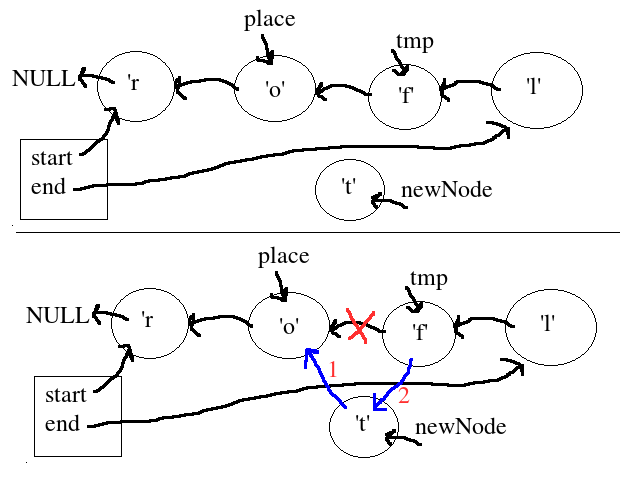
Our task is to implement the append() operation for this form of linked list. In pictures, our task is as follows:

The familiar “place” and “newNode” references are kept for continuity with our in-class and project examples, and we see that in order to perform the proper connections, we need to also set a pointer to the node “after” place.

The setting of tmp will require a loop and logic similar to our getpos()/setpos() functions, and to the astute, the procedure actually resembles that of insert() in our next-oriented singly-linked list. And such observations would be in no way incorrect.

In math, we are familiar with the impact multiplying by -1 can have on an equation (especially in terms of + and - values):

-1(x^2 + 3x - 9) becomes -x^2 - 3x + 9

In logic, we've seen operation changes as a result of applying demorgan's laws:

~(P ^ Q) can be expressed as ~P V ~Q

So, positive becomes negative, plus becomes minus. All inclusive becomes conditionally inclusive (and vice versa).

Here with the previous-oriented linked-list, we have the same concept at work. While we