As abstraction is a key focus of Computer Science and Data Structures, our first knowledge assessment, dska0, presented an activity befitting of such concepts.

Taking a page from our on-going linked list explorations, this activity presented a modified linked list, specifically of the form:

struct node {
    unsigned char data;
    struct node *prev;
};

That is, a singly-linked node that is intended to linked to its previous neighbor, vs. its next neighbor, as the bulk of our in-class examples and projects have focused on.

So from an implementation point-of-view, yeah, a bit different (inverted, even), but conceptually? No different at all.

To make sure we understand the scope of what was being asked, we were to implement (at a minimum) the append() operation for this previous-oriented singly-linked list.

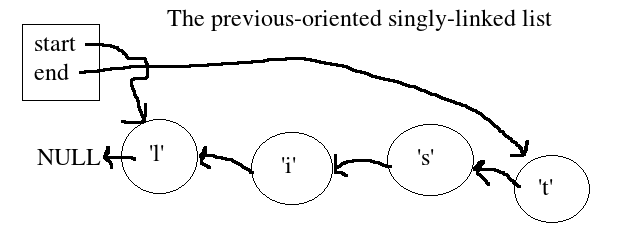
I drew a similar picture on the board of how the list is manifested:

Note that the NULL terminating the list is to the left of the list start… so again, an inversion or negation of what we are used to seeing.

The trick here is that we still “view” this list from left to right– start is on the left (or beginning), and end is on the right (the contextual end). In this scenario, the connections work against the grain when using the list.

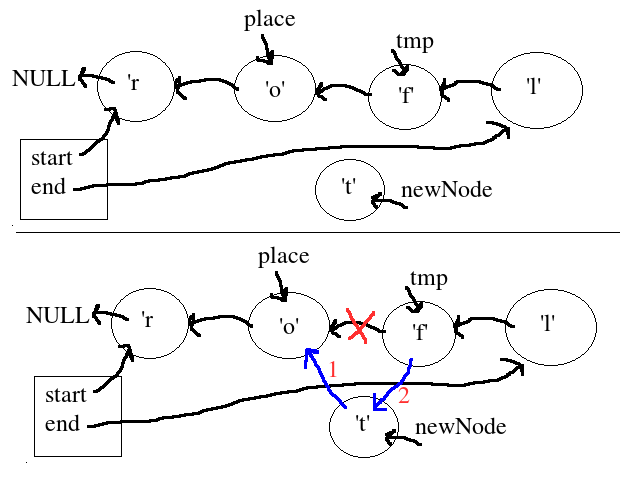
Our task is to implement the append() operation for this form of linked list. In pictures, our task is as follows:

The familiar “place” and “newNode” references are kept for continuity with our in-class and project examples, and we see that in order to perform the proper connections, we need to also set a pointer to the node “after” place.

The setting of tmp will require a loop and logic similar to our getpos()/setpos() functions, and to the astute, the procedure actually resembles that of insert() in our next-oriented singly-linked list. And such observations would be in no way incorrect.

In math, we are familiar with the impact multiplying by -1 can have on an equation (especially in terms of + and - values):

-1(x^2 + 3x - 9) becomes -x^2 - 3x + 9

In logic, we've seen operation changes as a result of applying demorgan's laws:

~(P ^ Q) can be expressed as ~P V ~Q

So, positive becomes negative, plus becomes minus. All inclusive becomes conditionally inclusive (and vice versa).

Here with the previous-oriented linked-list, we have the same concept at work:

• insert() in a next-oriented singly-linked list is functionally equivalent to append() in a previous-oriented singly-linked list
• append() in a next-oriented singly-linked list is functionally equivalent to insert() in a previous-oriented singly-linked list
• To display the list from start to end in a previous-oriented singly-linked list, we effectively need to use the displayb() logic to assist us in our task.

More precisely, to convert the next-oriented linked-list insert() into a previous-oriented linked-list append():

• all next references become prev
• all references to start become end
• all original references to end become start

You'll see that, instead of seeking from the start of the list, we must seek from the end. And just as with next-insert(), which requires us to get to the node “before”, prev-append() has the same need (it is the node that connects to place, and we get here from the end of the list).

The only difference here (if we were to implement getpos()/setpos() functionality), is that when considering list position values, instead of doing:

// next-oriented insert() tmp placement
tmp = setpos(theList, getpos(theList, place)-1);

We instead need to:

// prev-oriented append() tmp placement
tmp = setpos(theList, getpos(theList, place)+1);

Note the -1 and +1 difference.

Obviously, since getpos()/setpos() functions were not provided, some sort of repetition is in order (many seemed to go with a while loop, starting from the end of the list– an excellent choice).

Likely, something of the form:

tmp = myList -> end;
while (tmp -> prev != place)
{
    tmp = tmp -> prev;
}

And then we could perform the necessary hook-ups (average case consideration):

newNode -> prev = place;
tmp -> prev = newNode;

As for edge cases, aside from dealing with similar NULL and empty list scenarios, the edge cases for prev-append() would be the same as those considered in next-insert().

• next-insert() had special consideration for inserting before the start of the list
• prev-append() therefore has special consideration for appending after the end of the list

Similarly, as we just observed with the while loop logic:

• next-insert() had to locate the node one list position prior to place (coming from the direction of theList → start)
• prev-append() therefore has to locate the node one list position after place (coming from the direction of theList → end)

To aid in understanding, here is my reference implementation of append() for the previous-oriented singly-linked list:

1

#include "list.h"
 
//////////////////////////////////////////////////////////////////////
//
// append() - add newNode to the list after place
//
List *append(List *theList, Node *place, Node *newNode)
{
    //////////////////////////////////////////////////////////////////
    //
    // tmp will be our "after" pointer, allowing the side of the list
    // to the right of place to connect in to newNode
    //
    Node *tmp                   = NULL;
 
    //////////////////////////////////////////////////////////////////
    //
    // edge case: should the list pointer be NULL, allocate a new List
    //            and initialize theList -> start and end to sane
    //            initial values. This is essentially what mklist()
    //            does in the sll projects.
    //
    if (theList                == NULL)
    {
        theList                 = (List *) malloc(sizeof(List));
        theList -> start        = NULL;
        theList -> end          = NULL;
    }
 
    //////////////////////////////////////////////////////////////////
    //
    // edge case: the only thing that can gum up the works now is a
    //            NULL newNode; so if one is encountered, do nothing
    //            and return the list as-is.
    //
    if (newNode                != NULL)
    {
        //////////////////////////////////////////////////////////////
        //
        // edge case: if we have an empty list, newNode becomes the
        //            list contents.
        //
        if ((theList -> start  == NULL) &&
            (theList -> end    == NULL))
        {
            //////////////////////////////////////////////////////////////
            //
            // this is the simplest case- nothing exists so newNode IS
            // the list contents. Merely update the start and end
            // pointers and we're all set.
            //
            theList -> start    = newNode;
            theList -> end      = newNode;
        }
 
        //////////////////////////////////////////////////////////////
        //
        // edge case: if we're appending after end, we need to take
        //            care to update theList -> end
        //
        else if (place         == theList -> end)
        {
            //////////////////////////////////////////////////////////////
            //
            // this is the next simplest case to connect, as we only have
            // to deal with one connection (hooking newNode into the list;
            // then update theList -> end as appropriate).
            //
            newNode -> prev     = theList -> end;
            theList -> end      = newNode;
        }
 
        //////////////////////////////////////////////////////////////
        //
        // average case: if we're dealing with a typical append, we
        //               do the following. We're also protecting 
        //               against a rogue edge case of the list being
        //               non-empty yet place being NULL (trying to
        //               process that condition would result in 
        //               certain disaster).
        //
        else if (place         != NULL)
        {
            //////////////////////////////////////////////////////////////
            //
            // positioning tmp: we can only navigate from the end of the
            //                  list, so we must start tmp there; then,
            //                  keep seeking until we arrive at the node
            //                  one prev away from place.
            //
            tmp                 = theList -> end;
            while (tmp -> prev != place)
            {
                tmp             = tmp -> prev;
            }
 
            //////////////////////////////////////////////////////////////
            //
            // connecting it: newNode connects to place, and the existing
            //                list node connecting to place hooks to
            //                newNode.
            //
            newNode -> prev     = place;
            tmp     -> prev     = newNode;
        }
    }
 
    //////////////////////////////////////////////////////////////////
    //
    // whether we modify the list or bail out, we'll always return
    // the right thing.
    //
    return(theList);
}