Table of Contents

Corning Community College

CSCS2330 Discrete Structures

PROJECT: Prime Number Computation (PNC1)

OBJECTIVE

Taking your naive/brute force trial-by-division prime number program from pnc0, implement some algorithmic optimizations and analysis its improvements to performance over similar workloads.

TASK

Implement program in Vircon32 C, that:

REFERENCE

The following are reference screenshots of what your implementations should approximate.

PNC1

C implementation

EDIT

You will want to go here to edit and fill in the various sections of the document:

PNCX

algorithm: brute force / trial-by-division

variant: naive

The naive implementation is our baseline: implement with no awareness of potential tweaks, improvements, or optimizations. This should be the worst performing when compared to any optimization. 

START TIMEKEEPING
NUMBER: FROM 2 THROUGH UPPERBOUND:
    ISPRIME <- YES
    FACTOR: FROM 2 THROUGH NUMBER-1:
        SHOULD FACTOR DIVIDE EVENLY INTO NUMBER:
            ISPRIME <- NO
    PROCEED TO NEXT FACTOR
    SHOULD ISPRIME STILL BE YES:
        INCREMENT OUR PRIME TALLY
PROCEED TO NEXT NUMBER
STOP TIMEKEEPING
variant: break on composite (BOC)

just add a break; statement within your brute loop like so: 

START TIMEKEEPING
NUMBER: FROM 2 THROUGH UPPERBOUND:
    ISPRIME <- YES
    FACTOR: FROM 2 THROUGH NUMBER-1:
        SHOULD FACTOR DIVIDE EVENLY INTO NUMBER:
            ISPRIME <- NO
            BREAK
    PROCEED TO NEXT FACTOR
    SHOULD ISPRIME STILL BE YES:
        INCREMENT OUR PRIME TALLY
PROCEED TO NEXT NUMBER
STOP TIMEKEEPING
variant: odds-only processing

Start at 3 and increment by two to get only odd numbers. Then add one to tally count to account for 2 like so: 

START TIMEKEEPING
NUMBER: FROM 3 THROUGH UPPERBOUND:
    ISPRIME <- YES
    FACTOR: FROM 3 THROUGH NUMBER-1:
        SHOULD FACTOR DIVIDE EVENLY INTO NUMBER:
            ISPRIME <- NO
    PROCEED TO NEXT FACTOR BY TWO
    SHOULD ISPRIME STILL BE YES:
        INCREMENT OUR PRIME TALLY
PROCEED TO NEXT NUMBER BY TWO
ONCE UPPERBOUND IS REACHED ADD A ONE TO YOUR PRIME TALLY TO ACCOUNT FOR NOT STARTING AT TWO
STOP TIMEKEEPING
variant: sqrt point

Say you're using i for the outer loop and j for the inner loop, now rather that j < i you want j * j < = i 

START TIMEKEEPING
NUMBER: FROM 2 THROUGH UPPERBOUND:
    ISPRIME <- YES
    FACTOR: FROM 2 * 2 THROUGH NUMBER-1:
        SHOULD FACTOR DIVIDE EVENLY INTO NUMBER:
            ISPRIME <- NO
    PROCEED TO NEXT FACTOR BY TWO
    SHOULD ISPRIME STILL BE YES:
        INCREMENT OUR PRIME TALLY
PROCEED TO NEXT NUMBER BY TWO
ONCE UPPERBOUND IS REACHED ADD A ONE TO YOUR PRIME TALLY TO ACCOUNT FOR NOT STARTING AT TWO
STOP TIMEKEEPING
variant: break+odds
START TIMEKEEPING
NUMBER: FROM 3 THROUGH UPPERBOUND:
    ISPRIME <- YES
    FACTOR: FROM 3 THROUGH NUMBER-1:
        SHOULD FACTOR DIVIDE EVENLY INTO NUMBER:
            ISPRIME <- NO
            BREAK
    PROCEED TO NEXT FACTOR BY TWO
    SHOULD ISPRIME STILL BE YES:
        INCREMENT OUR PRIME TALLY
PROCEED TO NEXT NUMBER BY TWO
ONCE UPPERBOUND IS REACHED ADD A ONE TO YOUR PRIME TALLY TO ACCOUNT FOR NOT STARTING AT TWO
STOP TIMEKEEPING
variant: break+sqrt

Same as sqrt but add a break 

START TIMEKEEPING
NUMBER: FROM 2 THROUGH UPPERBOUND:
    ISPRIME <- YES
    FACTOR: FROM 2 * 2 THROUGH NUMBER-1:
        SHOULD FACTOR DIVIDE EVENLY INTO NUMBER:
            ISPRIME <- NO
            BREAK
    PROCEED TO NEXT FACTOR BY TWO
    SHOULD ISPRIME STILL BE YES:
        INCREMENT OUR PRIME TALLY
PROCEED TO NEXT NUMBER BY TWO
ONCE UPPERBOUND IS REACHED ADD A ONE TO YOUR PRIME TALLY TO ACCOUNT FOR NOT STARTING AT TWO
STOP TIMEKEEPING
variant: break+odds+sqrt

For this version, you will combine all three of the above into one process!

ALGORITHM: sieve of eratosthenes

variant: baseline soe

The sieve of Eratosthenes is one of the best algorithms for finding prime numbers, you may have noticed that up to this point all the code we have written has a complexity of O(n^2). The soe takes the next step and goes to O(nlog(log(n)).

Here is how the Sieve of Eratosthenes works:

First, you start with 2, and count up to your upper bound. For this example, let's say it is 40: 

    2  3  4  5  6  7  8  9 10
11 12 13 14 15 16 17 18 19 20
21 22 23 24 25 26 27 28 29 30
31 32 33 34 35 36 37 38 39 40

Then, you go through the list and remove multiples of 2. After that, you go to the next remaining number, which you now know is prime. Then, you remove multiples of that number, and so on.

To continue from above, 2 is a prime number, so you leave it alone, and remove any multiples of 2: 

    2  3     5     7     9  
11    13    15    17    19  
21    23    25    27    29  
31    33    35    37    39

Then, you go to the next number: 3. Now you know 3 is a prime number, so you can remove multiples of 3: 

    2  3     5     7        
11    13          17    19  
      23    25          29  
31          35    37

You go through the entire list, and when you get to the end, you are only left with prime numbers: 

    2  3     5     7        
11    13          17    19  
      23                29  
31                37        
START TIMEKEEPING
NUMBER: FROM 2 THROUGH UPPERBOUND:
    SHOULD THE NUMBER SLOT BE TRUE:
        VALUE AT NUMBER IS PRIME, INCREMENT TALLY
        MULTIPLE: FROM NUMBER+NUMBER THROUGH UPPERBOUND:
            VALUE AT MULTIPLE IS NOT PRIME
            MULTIPLE IS MULTIPLE PLUS NUMBER
        PROCEED TO NEXT MULTIPLE
    INCREMENT NUMBER
PROCEED TO NEXT NUMBER
STOP TIMEKEEPING
variant: sieve of eratosthenes with sqrt trick (soes)
START TIMEKEEPING
NUMBER: FROM 2 THROUGH NUMBER*NUMBER<UPPERBOUND:
    SHOULD THE NUMBER SLOT BE TRUE:
        VALUE AT NUMBER IS PRIME, INCREMENT TALLY
        MULTIPLE: FROM NUMBER*NUMBER THROUGH UPPERBOUND:
            VALUE AT MULTIPLE IS NOT PRIME
            MULTIPLE IS MULTIPLE PLUS NUMBER
        PROCEED TO NEXT MULTIPLE
    INCREMENT NUMBER
PROCEED TO NEXT NUMBER
STOP TIMEKEEPING

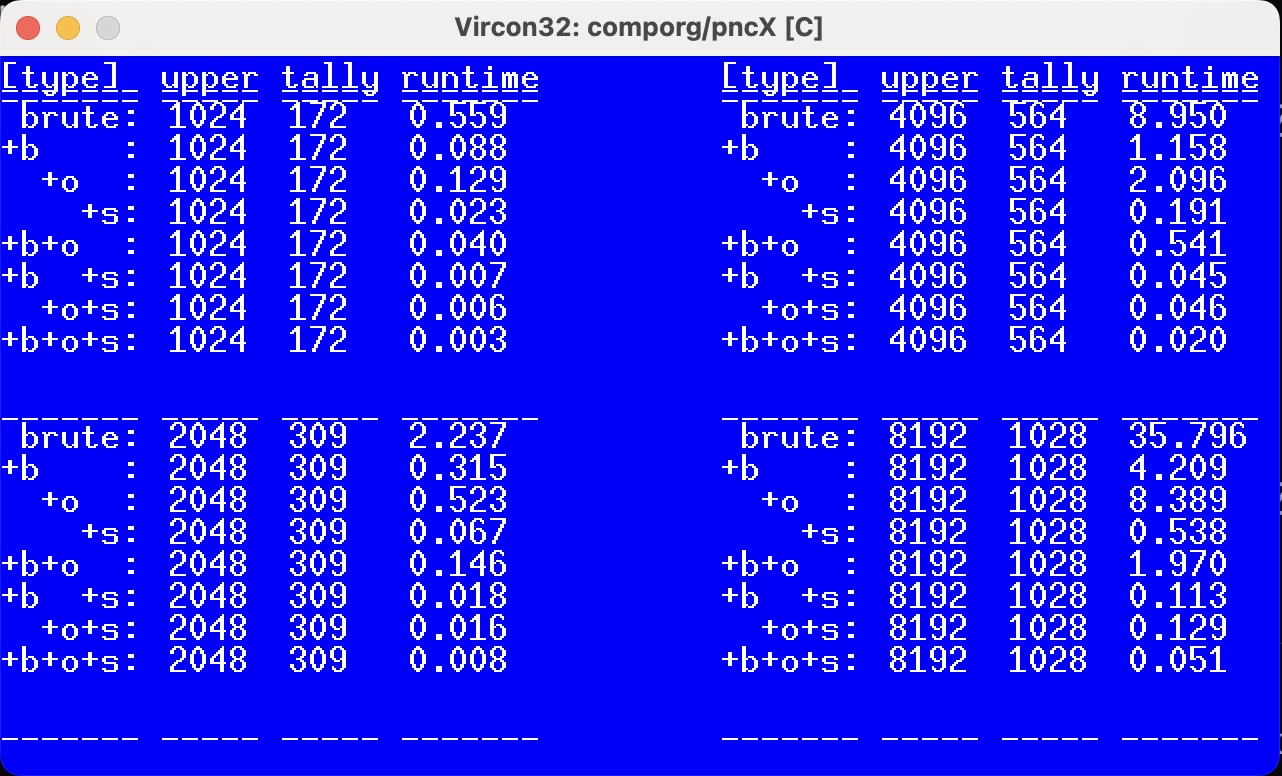
timing

wedge pnc1 runtimes

cgrant9 pnc1 runtimes

VerbalGnat48's pnc1 runtimes

MrVengeance's pnc1 runtimes

XaViEr'S pnc1 runtimes

Cburling's pnc1 runtimes

Blaize Patricelli pnc1 runtimes

 

SUBMISSION

To be successful in this project, the following criteria (or their equivalent) must be met:

Submit Tool Usage

Let's say you have completed work on the project, and are ready to submit, you would do the following: 

lab46:~/src/SEMESTER/DESIG/PROJECT$ submit DESIG PROJECT file1 file2 file3 ... fileN

You should get some sort of confirmation indicating successful submission if all went according to plan. If not, check for typos and or locational mismatches.

RUBRIC

I'll be evaluating the project based on the following criteria: 

208:pnc1:final tally of results (208/208)
*:pnc1:code, XML, build script, and cartridge submitted [26/26]
*:pnc1:processing and output is correct, and to specifications [26/26]
*:pnc1:break on composite optimization present and functional [26/26]
*:pnc1:odds only processing optimization present and functional [26/26]
*:pnc1:sqrt trick processing optimization present and functional [26/26]
*:pnc1:graph produced from timing data produced of all 8 variants [26/26]
*:pnc1:graph posted to discord and documentation page [26/26]
*:pnc1:timing data is the taken out to at least 4 decimal places [26/26]

Pertaining to the collaborative authoring of project documentation

Additionally