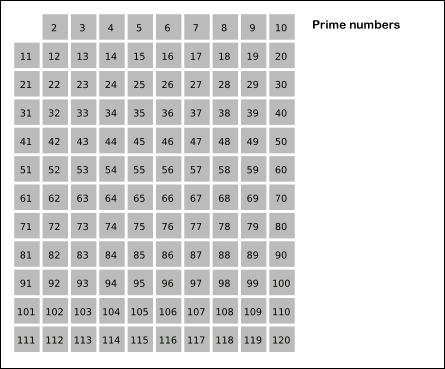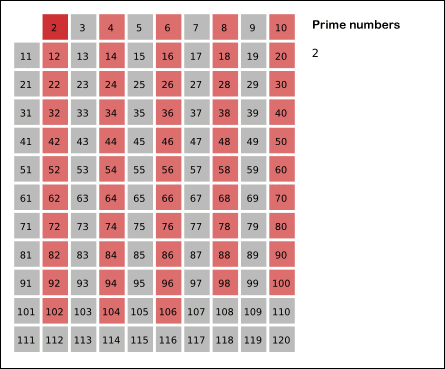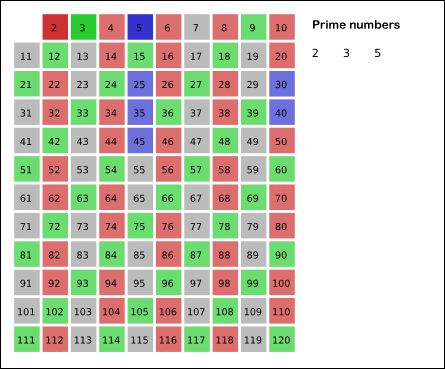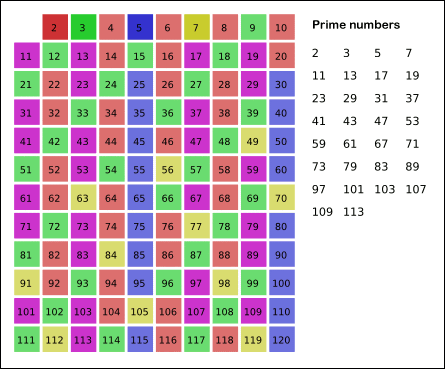
Table of Contents

Corning Community College

CSCS2330 Discrete Structures

~~TOC~~

Project: ALGORITHMS AND OPTIMIZATIONS - PRIME NUMBER COMPUTATION (pnc2)

Errata

With any increasingly complex piece of code or environment, we must find effective means of organizing various processes or communications. This “Errata” section and related updates are one such instance of that; intended as a means of disseminating information on changes to the project, you can be informed what modifications have taken place, along with any unique actions you need to take to compensate.

Any typos, bugs, or other updates/changes to the project will be documented here.

Revision List

Some changes may involve updates being made available to the project, in which case you'll be prompted with such notification and can run the available updating commands to synchronize your copy of the project with the changes.

Objective

To explore fundamentally different approaches in algorithm to a familiar theme. Also, to explore, where applicable, how some existing optimizations can be integrated.

Algorithmic Complexity

A concept in Computer Science curriculum is the notion of computational/algorithmic complexity.

Basically, for our current purposes, a solution to a problem exists on a spectrum of efficiency (typically constrained by time or space). Once you've hashed out an implementation:

Let it be clear: using modern computers bound by these so-called fourth dimensional constraints, we cannot write solutions without some foothold in both space and time (any program has statements in it that accomplish the task at hand (space occupied), and that same program takes time to run (even if it happens rather quickly)). What we can do is influence where on the space-time spectrum our implementation falls, and if done strategically for the particular constraint at hand, can aid us in achieving desired improvements in program efficiency.

In the previous projects, we focused on algorithms that were more constrained by time- taking progressively more time the larger the data set to be processed became. These time-constrained algorithms also happen to be the type of algorithm you're most familiar with (or at least, were indoctrinated into thinking with…). Your third grade self, on the other hand, potentially would have found more familiarity with the space-constrained methods this project will explore.

So in contrast to time-constrained approaches, we have some space-constrained approaches, which will utilize more space (ie allocating memory) in the solving of the program to the benefit of requiring less time (as compared to the time-constrained approaches, which will likely have a far smaller memory footprint at run-time).

As I said above, we can never be entirely time- or space-free… some element of both will always be present in our solutions. But by embracing the advantages of an approach, we can really make an impact in the desired area.

What we will be looking at in this project is a type of prime number calculating algorithm known as a sieve. It will make strategic use of space to aid us in the solving of the problem instead of exclusively relying on time.

Of note, the “mainstream” prime number computing efforts typically make use of sieves in some part of their strategy.

Optimizing the prime number calculation

Following will be the optimized algorithms I'd like you to implement for comparison with all the others.

For this project, please assume the following:

But, the conceptual level, at least for the baseline implementation, what we'll be pursuing will be the space-based equivalent of primereg, that is, no fancy optimizations for odd numbers, no map traversals, nor the sqrt() tricks, just straight up processing of the values that need to be processed.

You may find some of the previous optimizations aren't even applicable based on how this algorithm works (break on composite, for instance).

Sieve of Eratosthenes (primesoe)

Your next program, and first sieve, will be the Sieve of Eratosthenes. Perhaps among the best and likely longest-known sieves, its origins date from antiquity.

This sieve, instead of calculating to determine the eligibility of a prime, works in a manner of marking off patterns of values that cannot be prime (so, it is composite-focused in approach vs. prime-focused).

In order for it to work, we must store all the values we're processing so we can obtain what is left when done– what remains are the prime values.

Here is the wikipedia page: https://en.wikipedia.org/wiki/Sieve_of_Eratosthenes

Here is an animated image of this sieve in action (from wikipedia):

This YouTube video may also be helpful:

Sieve of Eratosthenes

A basic outline of the algorithm (again, from the wikipedia page):

Overview of Algorithm

To find all the prime numbers less than or equal to a given integer n by Eratosthenes' method:

  1. Create a list of consecutive integers from 2 through n: (2, 3, 4, …, n).
  2. Initially, let p equal 2, the smallest prime number.
  3. Enumerate the multiples of p by counting to n from 2p in increments of p, and mark them in the list (these will be 2p, 3p, 4p, … ; the p itself should not be marked).
  4. Find the first number greater than p in the list that is not marked. If there was no such number, stop. Otherwise, let p now equal this new number (which is the next prime), and repeat from step 3.

When the algorithm terminates, the numbers remaining in the list that are not marked are the primes below n.

Program Implementation

This is a space-constrained algorithm, therefore we will need a chunk of space to store these values. Think about what a lot of this looks like with respect to how you know how to organize data.

prime algorithm optimizations

To give us a decent appreciation of the subtleties of algorithm development in a theme of programs, I have identified the following optimizations that we will be implementing.

For simplicity, I have encoded this information in the file name (and therefore resulting executable/binary) that will correspond to the indicated algorithm+optimizations.

To break it down, all prime programs will be of the form:

The optimizations we will be implementing in this project (and their naming values) include:

Unless specified in the encoded name, your algorithm should only implement the algorithm and optimization(s) specified.

That is, if your program to implement is primesoeo, that means you are ONLY to implement the sieve of Eratosthenes algorithm and odds-only checking. NO sqrt() trick, etc. We are establishing separate data points for analytical comparison.

On the other hand, if your program to implement is primesoeos, that means your are implementing the “odds traversal”, and “sqrt() trick” optimizations.

Some of these optimizations can co-exist easily (odd + sqrt(), odd + approx square root), while others are mutually exclusive (sqrt() and approximated square root conflict). So there are definitely a few combinations that are possible using this scheme.

For this project, you'll be implementing various combinations of optimizations, giving us a full set of programs to analyze performance.

A note on comments

Something I noticed (and have historically noticed) in relation to comments that I'd like to point out:

Comments should be describing what is going on in your code.

With projects like this, often relying on a common base, comments become even more important, as they allow me to see specifically what is changed or unique about one variant over the other.

As such, when evaluating the project, I will be looking for pertinent comments specifically covering the how or why of the particular change unique to the variant in question.

And notice I said the “how” and/or “why”. NOT the “what”. I see all the time vague comments like “// doing the sqrt() optimization”… but:

These are things I'd like to see addressed in your comments, as there were some cases where the WHAT was claimed, yet what actually followed had little resemblance (if any) on the requirements for that variant.

Just like if you can't do it by hand you have no business trying to code it- if you cannot adequately explain the WHY and HOW, you similarly will have trouble.

Programs

It is your task to write the following Sieve of Eratosthenes-oriented prime number calculating programs:

Program Specifications

Your program should:

Implementation Restrictions

As our goal is not only to explore the more subtle concepts of computing but to promote different methods of thinking (and arriving at solutions seemingly in different ways), one of the themes I have been harping on is the stricter adherence to the structured programming philosophy/paradigm. It isn't just good enough to be able to crank out a solution if you remain blind to the many nuances of the tools we are using, so we will at times be going out of our way to emphasize focus on certain areas that may see less exposure (or avoidance due to it being less familiar– and from what I've witnessed so far this semester, avoidance is alive and well).

As such, the following implementation restrictions are also in place:

A common resistance or complaint I get with imposing these is that it may make your solutions more cumbersome or less optimal; that actually may not be an incorrect assertion, but remember: we are interested in the longer-term pursuit of structured thinking and effective problem solving. To foster your ability to think flexibly and differently. We tend to be naturally more averse to going against the grain, but to be an effective programmer/problem solver, this is absolutely necessary. It may be “annoying”, and you may choose to make it more aggravating on both yourself and me by agonizing over it, but history and experience teaching has shown me, time and time again, that this is an investment and it pays off in the long run (assuming one actually plays along).

I am seeking to make you all better thinkers and programmers, and I cannot do that if I cave to your innate desires not to change your ways of doing things. Yes, it may be unfamiliar; yes, it may be perceived as challenging. But you know what? Work through it and eventually it becomes the new normal- what was challenging is now no longer an issue.

Grabit Integration

For those familiar with the grabit tool on lab46, I have made some skeleton files and a custom Makefile available for this project.

To “grab” it: 

lab46:~/src/discrete$ grabit discrete pnc2
make: Entering directory '/var/public/SEMESTER/discrete/pnc2'
Commencing copy process for SEMESTER discrete project pnc2:
 -> Creating project pnc2 directory tree           ... OK
 -> Copying pnc2 project files                     ... OK
 -> Synchronizing pnc2 project revision level      ... OK
 -> Establishing sane file permissions for pnc2    ... OK

*** Copy COMPLETE! You may now go to the '/home/USER/src/discrete/pnc2' directory ***

make: Leaving directory '/var/public/SEMESTER/discrete/pnc2'
lab46:~/src/discrete$ cd pnc2
lab46:~/src/discrete/pnc2$

NOTE: You do NOT want to do this on a populated pnc2 project directory– it will overwrite files.

And, of course, your basic compile and clean-up operations via the Makefile.

Makefile operations

Makefiles provide a build automation system for our programs, instructing the computer on how to compile files, so we don't have to constantly type compiler command-lines ourselves. I've also integration some other useful, value-added features that will help you with overall administration of the project.

Basic operation of the Makefile is invoked by running the command “make” by itself. The default action is to compile everything in the project directory.

Additional options are available, and they are provided as an argument to the make command. You can see the available options by running “make help”: 

lab46:~/src/discrete/pnc2$ make help
******************[ Discrete Structures pnc2 Project ]******************
** make                     - build everything                        **
** make showerrors          - display compiler warnings/errors        **
** make debug               - build everything with debug symbols     **
** make checkqty            - runtime evaluation for qty              **
** make checkrange          - runtime evaluation for range            **
**                                                                    **
** make verifyqty           - check implementation for qty validity   **
** make verifyrange         - check implementation for range validity **
** make verifyall           - verify project specifications           **
**                                                                    **
** make link                - link in previous prime programs         **
** make delink              - remove links to previous prime programs **
**                                                                    **
** make save                - create a backup archive                 **
** make submit              - submit assignment (based on dirname)    **
**                                                                    **
** make update              - check for and apply updates             **
** make reupdate            - re-apply last revision                  **
** make reupdate-all        - re-apply all revisions                  **
**                                                                    **
** make clean               - clean; remove all objects/compiled code **
** make help                - this information                        **
************************************************************************
lab46:~/src/discrete/pnc2$

A description of some available commands include:

The various “check” options do a runtime performance grid, allowing you to compare timings between your implementations.

The various “verify” options do more aggressive checks, helping to ensure your project falls within stated project specifications.

Just another “nice thing” we deserve.

Command-Line Arguments

To automate our comparisons, we will be making use of command-line arguments in our programs.

header files

We don't need any extra header files to use command-line arguments, but we will need an additional header file to use the atoi(3) function, which we'll use to quickly turn the command-line parameter into an integer, and that header file is stdlib.h, so be sure to include it with the others: 

#include <stdio.h>
#include <stdlib.h>

setting up main()

To accept (or rather, to gain access) to arguments given to your program at runtime, we need to specify two parameters to the main() function. While the names don't matter, the types do.. I like the traditional argc and argv names, although it is also common to see them abbreviated as ac and av.

Please declare your main() function as follows: 

int main(int argc, char **argv)

There are two very important variables involved here (the types are actually what are important, the names given to the variables are actually quite, variable; you may see other references refer to them as things like “ac” and “av”):

The arguments are accessible via the argv array, in the order they were specified:

Additionally, let's not forget the argc variable, an integer, which contains a count of arguments (argc == argument count). If we provided argv[0] through argv[4], argc would contain a 5.

example

For example, if we were to execute the primeregbms program: 

lab46:~/src/discrete/pnc1$ ./primeregbms 128 1 2 2048

We'd have:

and let's not forget:

With the conditionally optional arguments as part of the program spec, for a valid execution of the program, argc could be a value anywhere from 3 to 5.

Simple argument checks

While there are a number of checks we should perform, one of the first should be a check to see if the minimal number of arguments has been provided: 

    if (argc < 3)  // if less than 3 arguments (program_name + quantity + argv[2] == 3) have been provided
    {
        fprintf(stderr, "%s: insufficient number of arguments!\n", argv[0]);
        exit(1);
    }

Since argv[3] (lower bound) and argv[4] (upper bound) are conditionally optional, it wouldn't make sense to check for them in the overall count. But we can and do still want to stategically utilize argc to determine if an argv[3] or argv[4] is present.

Grab and convert max

Finally, we need to put the argument representing the maximum quantity into a variable.

I'd recommend declaring a variable of type int.

We will use the atoi(3) function to quickly convert the command-line arguments into int values: 

    max  = atoi (argv[1]);

And now we can proceed with the rest of our prime implementation.

Allocating large arrays

Being new to arrays, you may not know it yet, but there is an upper bound to how big you can declare an array at compile time.

That is, using the conventional array declaration: 

data_type arrayname[size];

It is likely dependent on some combination of the execution environment (32-, 64-bit?) and the compiler, but in practice I've found things generally get unhappy if we try to request array sizes at some point beyond 1-4million elements (which makes sense, most processes in modern operating systems allocate a default stack size of 4-8MiB… if a short int is 2 bytes, how many consecutive short ints before you hit 4MiB?)

As we'll be needing array sizes considerably larger than this for the project (will we? If I could drop a hint: yes, we will), how do we get around this?

The answer: runtime memory allocation

We can allocate memory at run-time, which gives us the benefit of populating variables and performing equations to derive more specific values. This is also a rather powerful programming technique/ability to deploy in more complex programs, so keep it handy in your toolkits.

To do so, we ignore the fake facade that is the array, and treat it like it actually exists to the computer: a pointer.

So when you declare your array, instead of using the square bracket notation, do it as a pointer instead: 

datatype *array_name  = NULL;

THEN, later on in your program when it comes time to allocate the array, we use a memory allocation function, of which for our current purposes one of the following 2 could suit our needs:

So, if we wanted a 32768 element integer array, to show examples allocating with each function (you'd obviously only use one, whichever best fit your usage scenario): 

int *array_name  = NULL;
 
// using malloc()
array_name = (int *) malloc (sizeof(int) * 32768);
 
// using calloc()
array_name = (int *) calloc (32768, sizeof(int));

What else is going on here? What's with the parenthesis and the integer pointer?

That's a typecast, and is a way of telling the compiler to contort data IN THAT INSTANCE to a certain type (because it is a different type, other than what we want).

As it turns out, malloc() and calloc() both return raw memory, which in C is manifested as type void *; if our array is an integer pointer, we should be nice and cast it (apply the rules of an integer pointer to the raw memory, allowing the assignment to take place without the compiler whining– some compilers, depending on settings in place, may whine more than others).

With this, we can get around the compile time array limits, because by allocating memory at runtime, we're getting additional memory given to us, vs. trying to fit within the default initial allotment.

You should then be able to access it using regular array notation, or my preference: pointer arithmetic. 

// C array syntax for accessing 3rd element of array:
array_name[2]
 
// C pointer arithmetic syntax for accessing 3rd element of array:
*(array_name+2)

Approximating array size

The nature of utilizing an array for the sieves, as you will likely discover quickly, is that the sheer quantity of elements needed increments drastically as the desired quantity goes up, especially when shooting for a quantity.

For example, if we were seeking the first 32 primes: 

lab46:~/src/cprog/pnc2$ ./primereg 32 1
2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 83 89 97 101 103 107 109 113 127 131

… we would see that the 32nd prime is 131. For the Sieve of Eratosthenes to successfully work in this case, we'd need an array size of at least 132 (if we do the standard mapping of array element to actual number, where element 0 would correspond with the number 0, and element 131 would correspond with number 131; 0-131 = 132 elements).

But that number isn't immediately known (indeed, the nature of the distribution of prime numbers is the subject of considerable mathematical exploration, with many various proofs demonstrating different aspects of their distribution– don't believe me? Just google “distribution of primes” and read up for yourself). And short of some impressive looking and very calculus-requiring integral, there doesn't (at least from some of my searches) seem to be a decent algebraic expression we can use to come close.

And without this knowledge of the largest prime in the desired quantity, our sieve implementation (with the requirements as I have specified) is sort of at a standstill.

So how do we get around this? I propose a combination of accepting knowledge from a more aware source (me), and a little algebraic ingenuity. Let's hack ourselves an array size equation! (Do I hear a “heck yeah!” ? “HECK YEAH!”)

First, you can actually produce a lot of this data, from your pnc1 programs (technically pnc0 as well, but you'll be waiting a whole heck of a lot longer).

Let's take one of the purportedly best-running programs from pnc1 (primeregbmoa) and contort it into giving us the information that we need.

With a little bit of UNIX shell magic (again, I'm not expecting you to know this, so I'm just giving it to you, but from the abstract/conceptual level, you should be able to recognize things here like loops and output statements, and with some informed knowledge of shell syntax, see variables as well), we have the following:

1
# clear the screen
clear
 
# loop for a powers of 2 progression 32-4194304 (inclusive)
for((qty=32; qty<=4194304; qty*=2)); do
 
    # display the quantity lead-in information
    printf "[%7s] %7sth prime: " "${qty}" "${qty}"
 
    # obtain the last/largest prime in the specified quantity
    value=$(./primeregbmoa ${qty} 1 2>/dev/null | tr ' ' '\n' | tail -2 | head -1)
 
    # display it, along with calculating its approximate multiplier
    printf "%8s (x%s)\n" "${value}" $(echo "(${value}/${qty})+1" | bc -q)
done

We start with qty of 32, as that is the default starting point of “make check” (so why not; makes sense to work with what we've got). But there's still an unknown: the MAXIMUM quantity we'll need to deal with, especially in relation to “make check” (focus on “make check” execution, not to infinity). This is less available to you, short of just guessing some possible maximum.

I'm going to drop a hint: you'll very likely not be going beyond a quantity of 4194304 (at least with a “make check” cut-off limit of 1 second), so use THAT as your upper bound of quantity, and that is why I use that number in the shell script given above.

You don't have to worry about running said shell script, as the output is right here: 

[     32]      32th prime:      131 (x5)
[     64]      64th prime:      311 (x5)
[    128]     128th prime:      719 (x6)
[    256]     256th prime:     1619 (x7)
[    512]     512th prime:     3671 (x8)
[   1024]    1024th prime:     8161 (x8)
[   2048]    2048th prime:    17863 (x9)
[   4096]    4096th prime:    38873 (x10)
[   8192]    8192th prime:    84017 (x11)
[  16384]   16384th prime:   180503 (x12)
[  32768]   32768th prime:   386093 (x12)
[  65536]   65536th prime:   821641 (x13)
[ 131072]  131072th prime:  1742537 (x14)
[ 262144]  262144th prime:  3681131 (x15)
[ 524288]  524288th prime:  7754077 (x15)
[1048576] 1048576th prime: 16290047 (x16)
[2097152] 2097152th prime: 34136029 (x17)
[4194304] 4194304th prime: 71378569 (x18)

What we have is the following:

So from the data given above, we can see that a rough approximation of space needed for 32 primes would be 32*5 or 160 elements (131 falls nicely into 160).

For 1024 we have a multiplier of 8 (1024*8 = 8192, which 8161 safely fits into).

Okay, so we've got some raw numbers, we know the array size needed for the smallest quantity (32*5), we also know the array size needed for the likely largest quantity (4194304*18). So how do we handle the intermediaries?

As you can see, there is no a clean progression at play here, so no simple patterns we can play off of. I offer a few suggestions (and for the purposes of this project, any are acceptable):

For example, we see that since our max multiplier is 18, what if we did some factoring of 18? Say: 6, 12, 18?

We could rig up something like this: 

if (qty <= 128)
    array_size = qty * 6;
else if (qty <= 32768)
    array_size = qty * 12;
else
    array_size = qty * 18;

In general, though, this is just a mild annoyance in our quest to implement the sieve of Eratosthenes for quantities, so if you just hard code an 18, while certainly dirty, will get the job done for our current purposes (I will most certainly NOT hold it against you).

Make sense? Hopefully. And more-so: if you've been able to follow this, it is also indicative of your general level of comprehension: if you understand the overall problem, the specific issue, and can interact conceptually, that makes you a better problem solver/Computer Scientist/programmer.

And please, ASK QUESTIONS if something doesn't make sense.

Timing

Often times, when checking the efficiency of a solution, a good measurement (especially for comparison), is to time how long the processing takes.

In order to do that in our prime number programs, we are going to use C library functions that obtain the current time, and use it as a stopwatch: we'll grab the time just before starting processing, and then once more when done. The total time will then be the difference between the two (end_time - start_time).

We are going to use the gettimeofday(2) function to aid us in this, and to use it, we'll need to do the following:

header file

In order to use the gettimeofday(2) function in our program, we'll need to include the sys/time.h header file, so be sure to add it in with the existing ones: 

#include <stdio.h>
#include <stdlib.h>
#include <sys/time.h>

timeval variables

gettimeofday(2) uses a struct timeval data type, of which we'll need to declare two variables in our programs (one for storing the starting time, and the other for the ending time).

Please declare these with your other variables, up at the top of main() (but still WITHIN main()– you do not need to declare global variables). 

    struct timeval time_start; // starting time
    struct timeval time_end;   // ending time

Obtaining the time

To use gettimeofday(2), we merely place it at the point in our code we wish to take the time.

For our prime number programs, you'll want to grab the start time AFTER you've declared variables and processed arguments, but JUST BEFORE starting the driving loop doing the processing.

That call will look something like this: 

    gettimeofday(&time_start, 0);

The ending time should be taken immediately after all processing (and prime number output) is completed, and right before we display the timing information to STDERR: 

    gettimeofday(&time_end, 0);

Displaying the runtime

Once we have the starting and ending times, we can display this to the timing file pointer. You'll want this line: 

fprintf(timing, "%8.4lf\n",
time_end.tv_sec-time_start.tv_sec+((time_end.tv_usec-time_start.tv_usec)/1000000.0));

For clarity sake, that format specifier is “%8.4lf”, where the “lf” is “long float”, that is NOT a number 'one' but a lowercase letter 'ell'.

And with that, we can compute an approximate run-time of our programs. The timing won't necessarily be accurate down to that level of precision, but it will be informative enough for our purposes.

Execution

Your program output should be as follows (given the specified range): 

lab46:~/src/cprog/pnc2$ ./primesoe 32 1
2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 83 89 97 101 103 107 109 113 127 131
  0.000088
lab46:~/src/cprog/pnc2$

The execution of the programs is short and simple- grab the parameters, do the processing, produce the output, and then terminate.

Based on specifications, it should also be able to do the following (override quantity with lower/upper bounds): 

lab46:~/src/cprog/pnc2$ ./primesoe 48 1 4 18
5 7 11 13 17
  0.000080
lab46:~/src/cprog/pnc2$

And (shift the lower bound, but still count out 32 primes): 

lab46:~/src/cprog/pnc2$ ./primesoe 32 1 16
17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 83 89 97 101 103 107 109 113 127 131 137 139 149 151 157 163
  0.000087
lab46:~/src/cprog/pnc2$

And of course the same for the 3 variants, and the same error message reporting if invalid values are given.

Performance changes

You may notice a change with the sieves as compared to the other algorithms you've implemented with respect to performance- there will likely be a lower bound of performance, ie you have to exceed a certain threshold before the algorithm truly enters its power band, and then it may truly be a step-up in terms of performance.

Check Results

If you'd like to compare your implementations, I rigged up a Makefile checking rule called “make checkqty” and “make checkrange” which you can run to get a nice side-by-side runtime comparisons of your implementations.

In order to work, you MUST be in the directory where your pnc2 binaries reside, and must be named as such (which occurs if you ran make to compile them).

check qty

lab46:~/src/discrete/pnc2$ make checkqty
=========================================================
      qty   soe     soeo    soes    soea    soeos   soeoa
=========================================================
       32  0.0002  0.0002  0.0002  0.0002  0.0002  0.0002
       64  0.0002  0.0002  0.0002  0.0002  0.0002  0.0002
      128  0.0002  0.0002  0.0002  0.0002  0.0002  0.0002
      256  0.0003  0.0003  0.0003  0.0003  0.0003  0.0003
      512  0.0004  0.0003  0.0004  0.0004  0.0004  0.0003
     1024  0.0006  0.0005  0.0006  0.0006  0.0006  0.0005
     2048  0.0011  0.0010  0.0011  0.0010  0.0009  0.0008
     4096  0.0021  0.0018  0.0020  0.0019  0.0017  0.0017
     8192  0.0045  0.0039  0.0040  0.0038  0.0033  0.0034
    16384  0.0088  0.0077  0.0080  0.0079  0.0067  0.0069
...
  2097152  ------  ------  ------  ------  ------  ------
=========================================================
 verify:     OK      OK      OK      OK      OK      OK
=========================================================
lab46:~/src/discrete/pnc2$

When the runtime of a particular prime variant exceeds an upper threshold (1 second), it will be omitted from further tests, and a series of dashes will instead appear in the output.

If you don't feel like waiting, simply hit CTRL-c and the script will terminate.

check range

lab46:~/src/discrete/pnc2$ make checkrange
coming soon
lab46:~/src/discrete/pnc2$

Verification

I also include a validation check- to ensure your prime programs are actually producing the correct list of prime numbers. If the check is successful, you will see “OK” displayed beneath in the appropriate column; if unsuccessful, you will see “MISMATCH”.

Full Verification Compliance

There's also a more rigorous verification step you can take, which runs your programs through a series to tests to see if they conform to project specifications: 

lab46:~/src/discrete/pnc2$ make verifyall
coming soon
lab46:~/src/discrete/pnc2$

verifyall tests

The “verifyall” is an industrial grade verification; there are 13 specific tests performed, they are:

If you'd actually to see the output your program's output is being tested against, that can be found in the /usr/local/etc directory in the file primeTEST, where “TEST” is the name of the verify test mentioned above.

For example, if you wanted to see the intended output of the invnary test, that would be found in:

You could easily run your program with the stated arguments for the test, then use cat to display the test results and do a visual comparison.

In general

Analyze the times you see… do they make sense, especially when comparing the algorithm used and the quantity being processed? These are related to some very important core Computer Science considerations we need to be increasingly mindful of as we design our programs and implement our solutions. Algorithmic complexity and algorithmic efficiency will be common themes in all we do.

Submission

To successfully complete this project, the following criteria must be met:

To submit this program to me using the submit tool, run the following command at your lab46 prompt: 

lab46:~/src/discrete/pnc2$ make submit
Delinking ...
removed ‘errors’

Project backup process commencing

Taking snapshot of current project (pnc2)      ... OK
Compressing snapshot of pnc2 project archive   ... OK
Setting secure permissions on pnc2 archive     ... OK

Project backup process complete

Submitting discrete project "pnc2":
    -> ../pnc2-DATESTRING-HR.tar.gz(OK)

SUCCESSFULLY SUBMITTED

You should get that final “SUCCESSFULLY SUBMITTED” with no error messages occurring. If not, check for typos and or locational mismatches.

Evaluation Criteria

Grand total points: 

390:pnc2:final tally of results (390/390)

What I will be looking for (for each file): 

*:pnc2:primeALGO.c compiles cleanly, no compiler messages [4/4]
*:pnc2:primeALGO.c implements only specified algorithm [8/8]
*:pnc2:primeALGO.c consistent indentation throughout code [4/4]
*:pnc2:primeALGO.c relevant how and why comments in code [7/7]
*:pnc2:primeALGO.c code conforms to project specifications [4/4]
*:pnc2:primeALGO.c implementation free from restrictions [13/13]
*:pnc2:primeALGO runtime output conforms to specifications [4/4]
*:pnc2:primeALGO make checkqty test times within reason [4/4]
*:pnc2:primeALGO make checkrange test times within reason [4/4]
*:pnc2:primeALGO make verifyall tests succeed [13/13]